Overview
On the article, Fashion-MNIST exploring, I concisely explored Fashion-MNIST dataset.We can get access to the dataset from Keras and on this article, I’ll try simple classification by Edward.
Data
I’ll use Fashion-MNIST dataset. Fasion-MNIST is mnist like data set. You can think this as the fashion version of mnist. It is written that because mnist is too easy for classification and used too much, this data set was made. You can check the page to read the document of Fashion-MNIST.
About the detail, please check the article below.
Fashion-MNIST exploring
Fashion-MNIST is mnist-like image data set. Each data is 28x28 grayscale image associated with fashion. Literally, this is fashion version of mnist. I'm thinking to use this data set on small experiment from now on. So, for the future, I checked what kind of data fashion-MNIST is. Fasion-MNIST is mnist like data set.
Here, I’ll get the dataset from Keras. If the version of it is old, it doesn’t have the dataset. You can update it by following command on terminal.
pip install keras --upgradeEdward
Actually, I don’t know yet Edward well. I just grasp it as one of the PPLs and for variational inference, Gibbs sampling and Monte Carlo method. Personally, I think the point is variational inference.
Anyway, about the details, it is better to read the official tutorial and the thesis below.
Keras modeling
At first, I got the datasets from Keras and made simple model.
By same manner as mnist dataset loading, we can get fashion mnist dataset.
from keras.datasets import fashion_mnist
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()On this article, I don’t use convolutional neural network. For simple neural
network, I made the data flatten and normalized.
import numpy as np
x_train_flatten = np.array([x.flatten() for x in x_train]) / 256
x_test_flatten = np.array([x.flatten() for x in x_test]) / 256The following one is the example of making model to classify the fashion mnist data.
from keras.layers import Dense, Input
from keras.utils import np_utils
from keras.models import Model
# model
inputs = Input(shape=(x_train_flatten.shape[1],))
x = Dense(512, activation='relu')(inputs)
x = Dense(512, activation='relu')(x)
x = Dense(128, activation='relu')(x)
predictions = Dense(10, activation='softmax')(x)
model = Model(input=inputs, output=predictions)
model.compile(optimizer='SGD', loss='categorical_crossentropy', metrics=['accuracy'])
# train
history = model.fit(x_train_flatten, np_utils.to_categorical(y_train), epochs=50, batch_size=256, shuffle=True, validation_split=0.1)/Users/shu/.pyenv/versions/3.4.3/lib/python3.4/site-packages/ipykernel_launcher.py:12: UserWarning: Update your `Model` call to the Keras 2 API: `Model(inputs=Tensor("in..., outputs=Tensor("de...)`
if sys.path[0] == '':
Train on 54000 samples, validate on 6000 samples
Epoch 1/50
54000/54000 [==============================] - 6s 108us/step - loss: 1.3392 - acc: 0.6096 - val_loss: 0.8533 - val_acc: 0.7312
Epoch 2/50
54000/54000 [==============================] - 6s 103us/step - loss: 0.7596 - acc: 0.7490 - val_loss: 0.6710 - val_acc: 0.7688
Epoch 3/50
54000/54000 [==============================] - 6s 105us/step - loss: 0.6445 - acc: 0.7835 - val_loss: 0.5970 - val_acc: 0.7913
Epoch 4/50
54000/54000 [==============================] - 5s 97us/step - loss: 0.5850 - acc: 0.8031 - val_loss: 0.5506 - val_acc: 0.8112
Epoch 5/50
54000/54000 [==============================] - 5s 92us/step - loss: 0.5465 - acc: 0.8139 - val_loss: 0.5245 - val_acc: 0.8177
Epoch 6/50
54000/54000 [==============================] - 5s 94us/step - loss: 0.5213 - acc: 0.8216 - val_loss: 0.5160 - val_acc: 0.8225
Epoch 7/50
54000/54000 [==============================] - 5s 95us/step - loss: 0.5041 - acc: 0.8268 - val_loss: 0.4860 - val_acc: 0.8297
Epoch 8/50
54000/54000 [==============================] - 5s 99us/step - loss: 0.4887 - acc: 0.8298 - val_loss: 0.4756 - val_acc: 0.8317
Epoch 9/50
54000/54000 [==============================] - 5s 95us/step - loss: 0.4737 - acc: 0.8364 - val_loss: 0.4720 - val_acc: 0.8313
Epoch 10/50
54000/54000 [==============================] - 5s 96us/step - loss: 0.4655 - acc: 0.8371 - val_loss: 0.4534 - val_acc: 0.8392
Epoch 11/50
54000/54000 [==============================] - 5s 94us/step - loss: 0.4550 - acc: 0.8409 - val_loss: 0.4494 - val_acc: 0.8415
Epoch 12/50
54000/54000 [==============================] - 5s 96us/step - loss: 0.4465 - acc: 0.8443 - val_loss: 0.4408 - val_acc: 0.8458
Epoch 13/50
54000/54000 [==============================] - 5s 94us/step - loss: 0.4387 - acc: 0.8470 - val_loss: 0.4305 - val_acc: 0.8493
Epoch 14/50
54000/54000 [==============================] - 5s 99us/step - loss: 0.4325 - acc: 0.8479 - val_loss: 0.4350 - val_acc: 0.8470
Epoch 15/50
54000/54000 [==============================] - 5s 92us/step - loss: 0.4283 - acc: 0.8497 - val_loss: 0.4788 - val_acc: 0.8278
Epoch 16/50
54000/54000 [==============================] - 5s 97us/step - loss: 0.4218 - acc: 0.8522 - val_loss: 0.4232 - val_acc: 0.8497
Epoch 17/50
54000/54000 [==============================] - 5s 94us/step - loss: 0.4145 - acc: 0.8541 - val_loss: 0.4427 - val_acc: 0.8428
Epoch 18/50
54000/54000 [==============================] - 5s 94us/step - loss: 0.4110 - acc: 0.8569 - val_loss: 0.4110 - val_acc: 0.8533
Epoch 19/50
54000/54000 [==============================] - 5s 94us/step - loss: 0.4060 - acc: 0.8572 - val_loss: 0.4194 - val_acc: 0.8550
Epoch 20/50
54000/54000 [==============================] - 5s 95us/step - loss: 0.4015 - acc: 0.8598 - val_loss: 0.4035 - val_acc: 0.8563
Epoch 21/50
54000/54000 [==============================] - 5s 94us/step - loss: 0.3965 - acc: 0.8614 - val_loss: 0.4037 - val_acc: 0.8575
Epoch 22/50
54000/54000 [==============================] - 5s 95us/step - loss: 0.3897 - acc: 0.8643 - val_loss: 0.3991 - val_acc: 0.8583
Epoch 23/50
54000/54000 [==============================] - 5s 94us/step - loss: 0.3888 - acc: 0.8645 - val_loss: 0.4018 - val_acc: 0.8550
Epoch 24/50
54000/54000 [==============================] - 5s 94us/step - loss: 0.3868 - acc: 0.8640 - val_loss: 0.3904 - val_acc: 0.8607
Epoch 25/50
54000/54000 [==============================] - 5s 96us/step - loss: 0.3824 - acc: 0.8654 - val_loss: 0.3963 - val_acc: 0.8597
Epoch 26/50
54000/54000 [==============================] - 5s 94us/step - loss: 0.3780 - acc: 0.8669 - val_loss: 0.3897 - val_acc: 0.8628
Epoch 27/50
54000/54000 [==============================] - 5s 95us/step - loss: 0.3755 - acc: 0.8678 - val_loss: 0.4331 - val_acc: 0.8457
Epoch 28/50
54000/54000 [==============================] - 6s 107us/step - loss: 0.3726 - acc: 0.8689 - val_loss: 0.3834 - val_acc: 0.8643
Epoch 29/50
54000/54000 [==============================] - 6s 116us/step - loss: 0.3729 - acc: 0.8691 - val_loss: 0.3797 - val_acc: 0.8648
Epoch 30/50
54000/54000 [==============================] - 5s 96us/step - loss: 0.3665 - acc: 0.8712 - val_loss: 0.3864 - val_acc: 0.8663
Epoch 31/50
54000/54000 [==============================] - 5s 94us/step - loss: 0.3648 - acc: 0.8732 - val_loss: 0.3732 - val_acc: 0.8668
Epoch 32/50
54000/54000 [==============================] - 5s 99us/step - loss: 0.3611 - acc: 0.8728 - val_loss: 0.3972 - val_acc: 0.8628
Epoch 33/50
54000/54000 [==============================] - 5s 94us/step - loss: 0.3579 - acc: 0.8734 - val_loss: 0.3791 - val_acc: 0.8660
Epoch 34/50
54000/54000 [==============================] - 5s 95us/step - loss: 0.3543 - acc: 0.8756 - val_loss: 0.3712 - val_acc: 0.8672
Epoch 35/50
54000/54000 [==============================] - 6s 102us/step - loss: 0.3538 - acc: 0.8754 - val_loss: 0.3772 - val_acc: 0.8680
Epoch 36/50
54000/54000 [==============================] - 5s 99us/step - loss: 0.3511 - acc: 0.8769 - val_loss: 0.3767 - val_acc: 0.8692
Epoch 37/50
54000/54000 [==============================] - 5s 95us/step - loss: 0.3493 - acc: 0.8773 - val_loss: 0.3715 - val_acc: 0.8690
Epoch 38/50
54000/54000 [==============================] - 5s 101us/step - loss: 0.3457 - acc: 0.8774 - val_loss: 0.3632 - val_acc: 0.8692
Epoch 39/50
54000/54000 [==============================] - 5s 93us/step - loss: 0.3442 - acc: 0.8781 - val_loss: 0.3643 - val_acc: 0.8702
Epoch 40/50
54000/54000 [==============================] - 5s 96us/step - loss: 0.3397 - acc: 0.8802 - val_loss: 0.3637 - val_acc: 0.8697
Epoch 41/50
54000/54000 [==============================] - 5s 100us/step - loss: 0.3362 - acc: 0.8814 - val_loss: 0.3763 - val_acc: 0.8667
Epoch 42/50
54000/54000 [==============================] - 5s 97us/step - loss: 0.3370 - acc: 0.8811 - val_loss: 0.3700 - val_acc: 0.8693
Epoch 43/50
54000/54000 [==============================] - 5s 93us/step - loss: 0.3342 - acc: 0.8818 - val_loss: 0.3578 - val_acc: 0.8748
Epoch 44/50
54000/54000 [==============================] - 5s 100us/step - loss: 0.3325 - acc: 0.8825 - val_loss: 0.3603 - val_acc: 0.8697
Epoch 45/50
54000/54000 [==============================] - 6s 106us/step - loss: 0.3320 - acc: 0.8821 - val_loss: 0.3664 - val_acc: 0.8698
Epoch 46/50
54000/54000 [==============================] - 5s 99us/step - loss: 0.3261 - acc: 0.8855 - val_loss: 0.3809 - val_acc: 0.8625
Epoch 47/50
54000/54000 [==============================] - 5s 97us/step - loss: 0.3251 - acc: 0.8854 - val_loss: 0.3676 - val_acc: 0.8648
Epoch 48/50
54000/54000 [==============================] - 5s 95us/step - loss: 0.3233 - acc: 0.8852 - val_loss: 0.3492 - val_acc: 0.8745
Epoch 49/50
54000/54000 [==============================] - 5s 94us/step - loss: 0.3208 - acc: 0.8868 - val_loss: 0.3493 - val_acc: 0.8748
Epoch 50/50
54000/54000 [==============================] - 5s 98us/step - loss: 0.3200 - acc: 0.8860 - val_loss: 0.3491 - val_acc: 0.8737Check how the training went.
import matplotlib.pyplot as plt
def show_history(history):
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train_accuracy', 'test_accuracy'], loc='best')
plt.show()
show_history(history)
Edward modeling
By using Edward, we can see the parameters and accuracy from the viewpoint of probability.
For inference, I wrote the code below.
import tensorflow as tf
import edward as ed
from edward.models import Normal, Categorical
D = x_train_flatten.shape[1]
x_ph = tf.placeholder(tf.float32, [None, D])
w = Normal(loc=tf.zeros([D, 10]), scale=tf.ones([D, 10]))
b = Normal(loc=tf.zeros(10), scale=tf.ones(10))
output = Categorical(tf.add(tf.matmul(x_ph, w), b))
w_q = Normal(loc=tf.Variable(tf.zeros([D, 10])),
scale=tf.nn.softplus(tf.Variable(tf.zeros([D, 10]))))
b_q = Normal(loc=tf.Variable(tf.zeros([10])),
scale=tf.nn.softplus(tf.Variable(tf.zeros([10]))))
y_ph = tf.placeholder(tf.int32, [None])
y_train_int = tf.cast(y_train, dtype=tf.int32)
inference = ed.KLqp({w: w_q, b:b_q}, data={x_ph: x_train_flatten, output: y_ph})
inference.initialize()
tf.global_variables_initializer().run()
for _ in range(1000):
info = inference.update(feed_dict={y_ph: y_train})
inference.print_progress(info)1000/1000 [100%] ██████████████████████████████ Elapsed: 277s | Loss: 86933.344For classification, we can use categorical distribution. Actually, I’m still confused about how to use categorical distribution for classification on Edward.
When I tried to give y_train data to model directly, some types of error such as type occurred. So I just set placeholder for y_train. It gave placeholder to model and after that, gave y_train data to the placeholder. By some trials, I couldn’t avoid this not beautiful two step’s way.
Anyway, after the inference, we can check the sampled points and accuracy. Before, I have looked for a nice flow of checking this and the article below shows nice way.
Even this, I need to re-construct the model. Is there any way to avoid the re-construction for checking the output?
n_samples = 100
prob_lst = []
samples = []
w_samples = []
b_samples = []
for _ in range(n_samples):
w_samp = w_q.sample()
b_samp = b_q.sample()
w_samples.append(w_samp)
b_samples.append(b_samp)
prob = tf.nn.softmax(tf.matmul( tf.cast(x_test_flatten, tf.float32) ,w_samp ) + b_samp)
prob_lst.append(prob.eval())
sample = tf.concat([tf.reshape(w_samp,[-1]),b_samp],0)
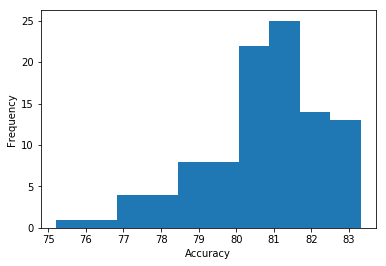
samples.append(sample.eval())The accurcy can be plotted.
accy_test = []
for prob in prob_lst:
y_trn_prd = np.argmax(prob,axis=1).astype(np.float32)
acc = (y_trn_prd == y_test).mean()*100
accy_test.append(acc)
plt.hist(accy_test)
plt.xlabel("Accuracy")
plt.ylabel("Frequency")
plt.show()