Bayesian prediction interval from pystan output

On this article, I’ll leave the simple memo to get bayesian prediction interval from the sampled points of PyStan output and visualize it.
Basically, I’ll use the code from the article, Simple Bayesian modeling by Stan.

import pandas as pd
import pystan

cars = pd.read_csv('cars.csv')
data = {'X':cars['speed'], 'Y':cars['dist'], 'N':cars.shape[0]}
fit = pystan.stan(file='cars_generated.stan', data=data, seed=42)

Stan code is as followings. Only difference from the original code is the generated quantities block. The purpose of this article is to check bayesian prediction interval. So, I added the generated quantities block.

data{
    int N;
    real X[N];
    real Y[N];
}

parameters{
    real a;
    real b;
    real<lower=0> sigma;
}

model {
    for (i in 1:N){
        Y[i] ~ normal(a * X[i] + b, sigma);
    }
}
generated quantities{
    real y_pred[N];
    for (i in 1:N){
        y_pred[i] = normal_rng(a * X[i] + b, sigma);
    }
}

To get percentile points from the extracted sample points, we can use numpy’s percentile() function. The code below is to extract samples, to get percentile points and to visualize it.

import numpy as np
import matplotlib.pyplot as plt

samples = np.percentile(fit.extract(permuted=True)['y_pred'], q=[10, 50, 90], axis=0)

plt.plot(range(samples.shape[1]), samples[0])
plt.plot(range(samples.shape[1]), samples[1])
plt.plot(range(samples.shape[1]), samples[2])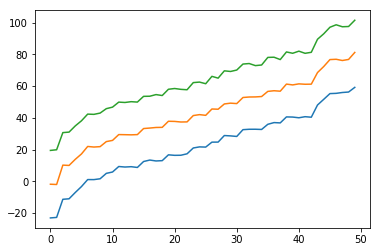

In this case, the plot is showing 10%, 50% and 90% lines.