By air passengers data, which is typical time-series data, I'll try some time-series analytics methods. Actually, about some points, I'm not sure if it is really appropriate or not. So, if you find some wrong or incorrect points, please let me know.

Data

Here, I'll use air passenger data, which is typical time-series data. You can download from the link below.

Air Passenger Data

To make the point simple, I don't download the data on the code. So, I'll just go on with the premise that the data is already on your working directory. Anyway, at first, import the necessary libraries and load data.

import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import pystan

data_loc = '/working_directory/AirPassengers.csv'
data = pd.read_csv(data_loc)

print(data.head())

     Month  #Passengers
0  1949-01          112
1  1949-02          118
2  1949-03          132
3  1949-04          129
4  1949-05          121

It has two columns and what I need is the second column, #Passengers. So, from now on, I’ll focus on #Passengers column. By visualization, we can see this is typical time-series data.

ts_data = data['#Passengers']
plt.plot(ts_data)
plt.show()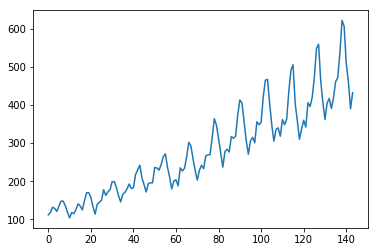

Stan codes

On this article, I'll try four types of Stan codes. The models are following four.

local level model
local trend model
local trend model for forecasting
local linear trend model for forecasting

If I organize those four just by the aspect of model type, I can say I'll try three types of models, local level model, local trend model and local linear trend model. The word “forecasting” concretely means that I generated random number based on the model for the future.

Mathematically, those are expressed as followings.

local level model

$y_t \sim Normal(u_t, \sigma_y^2)$
$u_t \sim Normal(u_{t-1}, \sigma_u^2)$

local trend model

$y_t \sim Normal(u_t, \sigma_y^2)$
$u_t \sim Normal(2\times u_{t-1}-u_{t-2} , \sigma_u^2)$

local linear trend model

$y_t \sim Normal(u_t, \sigma_y^2)$
$u_t \sim Normal(u_{t-1} + v_{t-1}, \sigma_u^2)$
$v_t \sim Normal(v_{t-1}, \sigma_v^2)$

local level model code

data {
    int N;
    vector[N] y;
    }

parameters {
    vector[N] u;
    real<lower=0> u_s;
    real<lower=0> y_s;
    }

model {
    u[2:N] ~ normal(u[1:N-1], u_s);
    y ~ normal(u, y_s);
}

local trend model code

data {
    int N;
    vector[N] y;
    }
parameters {
    vector[N] u;
    real<lower=0> u_s;
    real<lower=0> y_s;
    }
model {
    u[3:N] ~ normal(2 * u[2:N-1] - u[1:N-2], u_s);
    y ~ normal(u, y_s);
    }

local trend model for forecasting code

data {
    int N;
    int pred_Num;
    vector[N] y;
    }
parameters {
    vector[N] u;
    real<lower=0> u_s;
    real<lower=0> y_s;
    }
model {
    u[3:N] ~ normal(2 * u[2:N-1] - u[1:N-2], u_s);
    y ~ normal(u, y_s);
    }
generated quantities {
    vector[N + pred_Num] u_pred;
    u_pred[1:N] = u;
    for (t in 1:pred_Num){
        u_pred[N + t] = normal_rng(2*u_pred[N+t-1]-u_pred[N+t-2], u_s);
    }
}

local linear trend model for forecasting code

data {
    int N;
    vector[N] y;
    int pred_Num;
}

parameters {
    vector[N] u;
    vector[N] v;
    real<lower=0> s_u;
    real<lower=0> s_v;
    real<lower=0> s_y;
}

model {
    v[2:N] ~ normal(v[1:N-1], s_v);
    u[2:N] ~ normal(u[1:N-1]+v[1:N-1], s_u);
    y ~ normal(u, s_y);
}

generated quantities {
    vector[N + pred_Num] u_pred;
    vector[N + pred_Num] v_pred;
    vector[N + pred_Num] y_pred;
    u_pred[1:N] = u;
    v_pred[1:N] = v;
    y_pred[1:N] = y;
    for (t in 1:pred_Num){
        v_pred[N+t] = normal_rng(v_pred[N+t-1], s_v);
        u_pred[N+t] = normal_rng(u_pred[N+t-1]+v_pred[N+t-1], s_u);
    }
    for (t in 1:pred_Num){
        y_pred[N+t] = normal_rng(u_pred[N+t], s_y);
        }

}

Execute

We can execute the Stan code on Python by pystan.
At first, local model.

# local model
data_feed = {'N':ts_data.shape[0], 'y':ts_data}
fit_local_model = pystan.stan(file='local_model_1.stan', data=data_feed, iter=1000)

samples = fit_local_model.extract(permuted=True)
u_mean = samples['u'].mean(axis=0)

plt.plot(list(range(ts_data.shape[0])), ts_data)
plt.plot(list(range(len(u_mean))), u_mean)
plt.show()

Second, local trend model. As you can see, here I'm using same variable name by over writing. Practically, it is better to use other names.

# local trend model
fit_local_trend_model = pystan.stan(file='local_trend_model_1.stan', data=data_feed, iter=1000)

samples = fit_local_trend_model.extract(permuted=True)
u_mean = samples['u'].mean(axis=0)

plt.plot(list(range(ts_data.shape[0])), ts_data)
plt.plot(list(range(len(u_mean))), u_mean)
plt.show()

Third, local trend model for forecasting. On this model, predicted points made a calm line.

data_feed = {'N':ts_data.shape[0], 'y':ts_data, 'pred_Num': 100}
fit_local_trend_model = pystan.stan(file='local_trend_model_2.stan', data=data_feed, iter=1000)

samples = fit_local_trend_model.extract(permuted=True)
u_mean = samples['u_pred'].mean(axis=0)

plt.plot(list(range(ts_data.shape[0])), ts_data)
plt.plot(list(range(len(u_mean))), u_mean)
plt.show()

Fourth, local linear trend model for forecasting. Because I'm plotting the mean of the sampled points, we can see simple single line from the last observed points.

data_feed = {'N':ts_data.shape[0], 'y':ts_data, 'pred_Num': 100}
fit_local_linear_trend_model = pystan.stan(file='local_linear_trend_model.stan', data=data_feed, iter=1000)

samples = fit_local_linear_trend_model.extract(permuted=True)
u_mean = samples['u_pred'].mean(axis=0)

plt.plot(list(range(ts_data.shape[0])), ts_data)
plt.plot(list(range(len(u_mean))), u_mean)
plt.show()

About the term of the season, I'll try on next article.

Data Science Struggle

Monday, January 29, 2018

Simple trial of various types of time series analytics