Anti-pattern of the local level model with explanatory variable

Overview

On this article, I'll try anti-pattern of the local level model with explanatory variable.
Before, on the article, Local level model with explanatory variable to time series data on Stan , I made the local level model with explanatory variable to time series data. From the article, I set the model as followings.
$u_t \sim Normal(u_{t-1}, \sigma_ξ^2)$
$β_t \sim Normal(β_{t-1}, \sigma_τ^2)$
$y_t \sim Normal(u_t + β_t \times x_t, \sigma_e^2)$
There, I set state disturbances $σ_τ^2$ as zero. That’s because on the book, An Introduction to State Space Time Series Analysis (Practical Econometrics), it is written that these state disturbances are usually fixed on zero to establish a stable relationship between $y_t$ and $x_t$. This time, as experiment, I’ll try the model without setting $σ_τ^2$ as zero, meaning I’ll set $β_t$ as changeable.

Data

Before, I made the data with fixed slope $β$. This time, I'll make the $β$ changeable.

import numpy as np

# make data
np.random.seed(59)

x = np.random.normal(100, 5, 100)

data = []
u = []

u_start = 500.0
beta_start = 10.0

data.append(u_start + beta_start * x[0] + np.random.normal(0, 2))
u.append(u_start)
for i in range(100):
    if i == 0:
        u_temp = u_start
        beta_temp = beta_start
    else:
        next_u = u_temp + np.random.normal(0, 2)
        next_beta = beta_temp + np.random.normal(0, 5)

        data.append(next_u + next_beta * x[i] + np.random.normal(0, 2))
        u.append(next_u)

        u_temp = next_u
        beta_temp = next_beta

By visualization, we can check the data behavior.

import matplotlib.pyplot as plt
plt.plot(list(range(len(data))), data)

plt.show()

Stan Modeling

$β_t$ can change, depending on $β_{t-1}$.

data {
    int N;
    vector[N] X;
    vector[N] Y;
}

parameters {
    vector[N] u;
    vector[N] beta;
    real<lower=0> s_y;
    real<lower=0> s_u;
    real<lower=0> s_b;
}

transformed parameters {
    vector[N] y_hat;
    for(i in 1:N){
        y_hat[i] = u[i] + beta[i] * X[i];
    }
}

model {
    u[2:N] ~ normal(u[1:(N-1)], s_u);
    beta[2:N] ~ normal(beta[1:(N-1)], s_b);
    Y ~ normal(y_hat, s_y);
}

Execute on Python

On Python, we can execute sampling and check the outcome.

import pystan

data_feed = {'N': len(data), 'X': x, 'Y': data}
fit = pystan.stan(file='local_level_unstable.stan', data=data_feed, iter=1000)

samples = fit.extract(permuted=True)
beta_mean = samples['beta'].mean()
u_mean = samples['u'].mean(axis=0)

data_pred = u + beta_mean * x

plt.plot(list(range(len(data))), data)
plt.plot(list(range(len(data))), data_pred)
plt.show()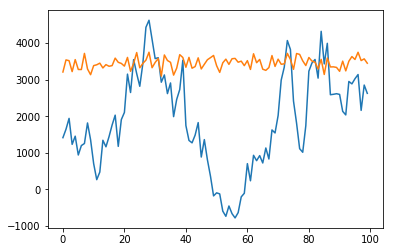

As you can see, the sampled points doesn't trace the data well.