Data Science Struggle: k-means++: Introduction and small experiment with Julia

Overview

On this article, I'll write about k-means++. To say precisely, I'll explain what k-means++ is and do small experiment with Julia. For the people who have experience of Python, Julia code is easy to read. So, basically no problem.
k-means++ is regarded as the algorithm to give nice initialization for k-means and sometimes can be used in other algorithm like EM algorithm.
If you find a mistake, please let me know on comment.

k-means++

k-means++ is the initialization method for k-means.
Before talking about k-means++ itself, I'll touch k-means. k-means is one of the clustering methods. By choosing the number of clusters, k, the algorithm does clustering to the data.
About the detail, please check the following articles.

Here, about k-means, I'll show the core points by the quotation from the article above.
k-means algorithm is very simple and intuitive.

Initialization

Optimization of representative points

Optimization of data points belonging

Initialization is done only once at first. The optimization of representative points and data points belongings repeat until the data points belongings become stable.

Initialization
As a premise, we assume that there are N data points and K clusters. On initialization phase, we randomly assign the cluster on the data points. To say precisely, we randomly assign cluster k (k∈1,..,K) on data n (n∈1,..,N).

Optimization of representative points
On the K-means algorithm, every cluster has its own representative point. The representative points are calculated as the mean of the data points which belong to the equivalent cluster.

Optimization of data points belonging
Every data point belongs to one cluster. The cluster which one specific data point belongs to depends on the distance between the representative points and the data point. The data point belongs to the nearest representative point.

The optimization of representative points and data points belonging will be repeated until it reaches convergence.
Briefly, k-means algorithm updates the center points(centroids) of the cluster in the loop.
As you can see, k-means algorithm can be separated into three parts, meaning initialization, optimization of representative points and optimization of data points belonging.
On the quotation above, I regarded just random assignment as initialization. But because two optimizations are repeated until it reaches convergence, it can be said that the first optimization of representative points(centroids) is also initialization. So, the quotation can also be expressed as below.

Initialization
As a premise, we assume that there are N data points and K clusters. On initialization phase, we randomly assign the cluster on the data points. To say precisely, we randomly assign cluster k (k∈1,..,K) on data n (n∈1,..,N).
The representative points are calculated as the mean of the data points which belong to the equivalent cluster.

Optimization of data points belonging
Every data point belongs to one cluster. The cluster which one specific data point belongs to depends on the distance between the representative points and the data point. The data point belongs to the nearest representative point.

Optimization of representative points
On the K-means algorithm, every cluster has its own representative point. The representative points are calculated as the mean of the data points which belong to the equivalent cluster.

The initialization includes first optimization of representative points(centroids) and the loop of optimizations start from optimization of data points belonging.
From here, I start to touch k-means++. k-means++ sounds something like better version of k-means, meaning better clustering method. But actually, this is initialization method. k-means++ suggests better way of initialization, to say precisely, better initial centroids to k-means.
The rule is as followings.
Assume the $X$ denotes the data and $x_i \in X$ .

randomly take $x_i$ from $X$ and set it as one of the centroids.
$D(x)$ denotes the distance between $x$ and the nearest centroid. Choose the next centroid from $X$ with probability $\frac{D(x)^2}{\sum_{x \in X}D(x)^2}$ .

Until the number of centroids reaches selected k, the second step is repeated.
This algorithm means that the point $x$ is chosen as centroid with high possibility when it is far from any existing centroids and with low possibility when it is near from the nearest centroid.
When it is used with k-means, basically, after k points are chosen by k-means++, usual k-means starts.
If you want to check the detail, I recommend to read the following paper.

http://ilpubs.stanford.edu:8090/778/1/2006-13.pdf

Code

The code of k-means with k-means++ is on my GitHub.

https://github.com/marubontan/Clustering/blob/master/src/kmeans.jl

I thought at first I would write the k-means++ part independently here. But it can be longer than my expectation. The code just follows the algorithm shown above. So, by using the code on GitHub, I’ll do experiment.

Experiments

At first, I'll focus only on k-means++ part. With low dimensional data, we can check it visually. I'll use the same artificial data as the Introduction to K-means: Algorithm and Visualization with Julia from scratch.
The code below will generate the data and visualize it.

using Distributions
using PyPlot
function makeData3D()
    groupOne = rand(MvNormal([10.0, 10.0, 10.0], 10.0 * eye(3)), 100)
    groupTwo = rand(MvNormal([0.0, 0.0, 0.0], 10 * eye(3)), 100)
    groupThree = rand(MvNormal([20.0, 20.0, 20.0], 10.0 * eye(3)), 100)
    return hcat(groupOne, groupTwo, groupThree)'
end

ThreeDimensionsData = makeData3D()

scatter3D(ThreeDimensionsData[1:100,1], ThreeDimensionsData[1:100,2], ThreeDimensionsData[1:100,3], color="red")
scatter3D(ThreeDimensionsData[101:200,1], ThreeDimensionsData[101:200,2], ThreeDimensionsData[101:200,3], color="blue")
scatter3D(ThreeDimensionsData[201:300,1], ThreeDimensionsData[201:300,2], ThreeDimensionsData[201:300,3], color="green")

A
s you can see, it is composed of three types of clusters. By the GIF image from the original article, we can see how centroids moved, meaning we can check how the initial values were.

From here, I’ll use k-means++. The code is from my GitHub.

https://github.com/marubontan/Clustering

After cloning it, we can use k-means++ part from the kmeans.jl. The k-means++ is written with k-means. But we can use k-means++ part independently.

include("./src/kmeans.jl")

Although the function name sounds bit ugly, don’t care. After including the kmeans.jl, we can execute the kMeansPlusPlus() function and get the initialized centroid points.

initializedCentroids = kMeansPlusPlus(DataFrame(ThreeDimensionsData), 3)
println(initializedCentroids)

Any[[2.55176, -2.94052, -2.86004], [10.315, 10.7338, 11.6187], [17.3163, 22.0337, 16.8082]]

I didn't set random number's seed. So, the outcome is not always same. Anyway, by visualizing those to the same space as the data points, we can know the behavior.

scatter3D(ThreeDimensionsData[:,1], ThreeDimensionsData[:,2], ThreeDimensionsData[:,3], color="blue", alpha=0.2)
one = [val[1] for val in initializedCentroids]
two = [val[2] for val in initializedCentroids]
three = [val[3] for val in initializedCentroids]

scatter3D(one, two, three, color="red")

If we compare this with the GIF image I showed, we can see that with k-means++ the initialized points reflects the clusters better. Be careful, the GIF image means the movement of centroids through k-means. So what we should focus is the first image of the GIF. That is the initialized points.

For now, we more or less know the k-means++ gives better initialization. Next, to the iris data and mnist data, we will check if the better initialization gives better accuracy or not. From the conclusion, I couldn’t see the better accuracy with those data.
In Julia, we can use popular data sets from some packages.

using RDatasets
iris = dataset("datasets", "iris")

To this iris data, we can use k-means and k-means with k-means++.

kmeansIrisResults = kMeans(iris[:, [:SepalLength, :SepalWidth, :PetalLength, :PetalWidth]], 3)
kmeansPPIrisResults = kMeans(iris[:, [:SepalLength, :SepalWidth, :PetalLength, :PetalWidth]], 3; initializer="kmeans++")

To check the accuracy, I'll write the function. On clustering, the estimated cluster number is random. So, to check the accuracy, we need to check which estimated class is responding to which class. Here, I wrote round-robin function for combination, although it is not efficient way.

using Combinatorics
using MLBase


function calculateAccuracy(groundTruth, predicted)
    maxCombination = []
    maxAccuracy = 0.0

    for combination in permutations(collect(Set(predicted)))
        conv = Dict()
        sortedGroundTruth = sort(collect(Set(groundTruth)))
        for pair in zip(sortedGroundTruth, combination)
            conv[pair[1]] = pair[2]
        end
        target = Array{Int}(length(groundTruth))
        for (i,label) in enumerate(groundTruth)
            target[i] = conv[label]
        end
        accuracy = correctrate(target, predicted)
        if accuracy > maxAccuracy
            maxAccuracy = accuracy
            maxCombination = combination
        end
    end
    return maxAccuracy
end

By using this function, I checked the accuracy.

speciesTemp = convert(Array, iris[:, [:Species]])
println(calculateAccuracy(speciesTemp, kmeansIrisResults.estimatedClass))
println(calculateAccuracy(speciesTemp, kmeansPPIrisResults.estimatedClass))

0.8866666666666667
0.8933333333333333

Actually, there is not apparent difference.
To check more carefully, I executed one thousand times and checked the distribution.

import Distances

srand(59)
kmeansIris = []
kmeansPPIris = []
for _ in 1:1000
    kmeansIrisResults = kMeans(iris[:, [:SepalLength, :SepalWidth, :PetalLength, :PetalWidth]], 3)
    kmeansPPIrisResults = kMeans(iris[:, [:SepalLength, :SepalWidth, :PetalLength, :PetalWidth]], 3; initializer="kmeans++")

    push!(kmeansIris, calculateAccuracy(speciesTemp, kmeansIrisResults.estimatedClass))
    push!(kmeansPPIris, calculateAccuracy(speciesTemp, kmeansPPIrisResults.estimatedClass))
end

Visualizing.

using PyPlot

plt[:hist](kmeansIris, color="blue", alpha=0.5)
plt[:hist](kmeansPPIris, color="red", alpha=0.5)
legend(["kmeans", "kmeans++"])

With Iris data, we can't say k-means++ is better. Rather, the outcome of k-means is better.
Aside to that, on this case, for the one thousand iteration, k-means and k-means++ takes following time.

kmeansTime = []
for _ in 1:1000
    time = @elapsed kmeansIrisResults = kMeans(iris[:, [:SepalLength, :SepalWidth, :PetalLength, :PetalWidth]], 3)
    push!(kmeansTime, time)
end

kmeansPlusPlusTime = []
for _ in 1:1000
    time = @elapsed kmeansPPIrisResults = kMeans(iris[:, [:SepalLength, :SepalWidth, :PetalLength, :PetalWidth]], 3; initializer="kmeans++")
    push!(kmeansPlusPlusTime, time)
end

Visualizing.

plt[:hist](kmeansTime, color="blue", alpha=0.5)
plt[:hist](kmeansPlusPlusTime, color="red", alpha=0.5)
legend(["kmeans", "kmeans++"])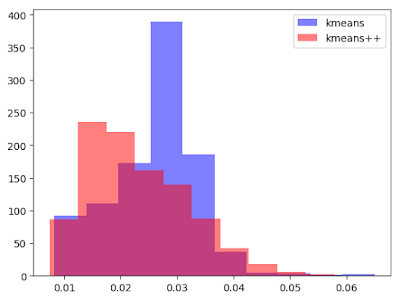

We can see the difference of distributions. k-means++ is faster.
To the MNIST dataset, I'll do same thing. It takes too much time to use all the data. So, I'll make subset of it.

using MLDatasets

train_x, train_y = MNIST.traindata()

sub_x = zeros(1000, 784)
for i in 1:1000
    sub_x[i, :] = vec(train_x[:,:,i])
end
sub_y = train_y[1:1000]

This time, I'll do clustering twenty times.

kmeansMnist = []
kmeansPPMnist = []
for _ in 1:20
    kmeansMnistResults = kMeans(DataFrame(sub_x), 10)
    kmeansPPMnistResults = kMeans(DataFrame(sub_x), 10; initializer="kmeans++")

    push!(kmeansMnist, calculateAccuracy(sub_y, kmeansMnistResults.estimatedClass))
    push!(kmeansPPMnist, calculateAccuracy(sub_y, kmeansPPMnistResults.estimatedClass))
end

Visualizing.

using PyPlot

plt[:hist](kmeansMnist, color="blue", alpha=0.5)
plt[:hist](kmeansPPMnist, color="red", alpha=0.5)
legend(["kmeans", "kmeans++"])

Hummmmmmm. Not so apparent difference. Let’s check the time.

kmeansMnistTime = []
for _ in 1:100
    time = @elapsed kMeans(DataFrame(sub_x), 10)
    push!(kmeansMnistTime, time)
end

kmeansPPMnistTime = []
for _ in 1:100
    time = @elapsed kMeans(DataFrame(sub_x), 10; initializer="kmeans++")
    push!(kmeansPPMnistTime, time)
end

Visualizing

plt[:hist](kmeansMnistTime, color="blue", alpha=0.5)
plt[:hist](kmeansPPMnistTime, color="red", alpha=0.5)
legend(["kmeans", "kmeans++"])

It looks nice. By k-means++, total time for clustering can be shorter and stable.

Reference

http://ilpubs.stanford.edu:8090/778/1/2006-13.pdf

Data Science Struggle

Saturday, May 5, 2018

k-means++: Introduction and small experiment with Julia

Overview

k-means++

Initialization

Optimization of representative points

Optimization of data points belonging

Initialization

Optimization of data points belonging

Optimization of representative points

Code

Experiments

Reference

Blog Archive